Quantization

Jooyoung Lee 2022. 12. 26. 17:43

2022. 12. 26. 17:43

원문 출처

양자화는 연속 데이터를 이산 숫자로 변환하는 과정이다.
신경망 훈련 계산은 일반적으로 Floating point type (16bit, 32bit)를 사용하여 수행된다.
딥러닝에서 양자화는 일반적으로 부동 소수점에서 고정 소수점 정수로 변환하는 것을 말한다.
딥러닝에서 사용되는 양자화 기술은 Dynamic Quantization, Static Quantization 등이 존재한다.

Quantization Mapping

양자화는 부동 소수점 값 $x \in [α, β]$ 를 b-bit 정수 $x_{q} \in [α_{q}, β_{q}]$ 에 맵핑한다.

de-Quantization 프로세스 수학적 정의

$x = c (x_{q} + d)$

Quantization 프로세스 수학적 정의

$x_{q} = r o u n d (\frac{1}{c} x - d)$

c, d : 변수(variables)

c 및 d를 유도하기 위하여 α가 αq에 대한 맵과 β가 βq 맵에 대한 맵을 확인하야하고, 선형 시스템 문제를 해결해야 한다.

$β = c (β_{q} + d)$

$α = c (α_{q} + d)$

솔루션은 다음과 같다.

$c = \frac{β - α}{β_{q} - α_{q}}$

$d = \frac{α β_{q} - β α_{q}}{β - α}$

실제로, 양자화 후 에러 없이 Floating point "0"이 정확하게 표현되도록 해야 한다.

수학적 증명 :

$x_{q} = r o u n d (\frac{1}{c} 0 - d)$

$= r o u n d (- d)$

$= - r o u n d (d)$

$= - d$

위 수식의 의미는 아래와 같다

$d = r o u n d (d)$

$= r o u n d (\frac{α β_{q} - β α_{q}}{β - α})$

컨벤션에 의해서 c를 스케일 s로 , -d를 zero point z로 표시한다.

요약

Quantization

$x = s (x_{q} - z)$

de-quantization

$x_{q} = r o u n d (\frac{1}{s} x + z)$

스케일 's' , Zero point 'z'의 값

$s = \frac{β - α}{β_{q} - α_{q}}$

$z = r o u n d (\frac{β α_{q} - α β_{q}}{β - α})$

'z'는 정수, 's'는 부동 소수점이다.

Value Clipping

실제로, 양자화 과정은 $[α, β]$ 의 범위를 벗어난 $x$ 를 가질 가능성이 있으며, 양자화 된 값 $x_{q}$ 또한 $[α, β]$ 의 범위를 벗어난다.
Integer type이 INTb 및 $(a l p h a_{q}, β_{q}) = (- 2^{b - 1}, 2^{b - 1} - 1)$ 또는 unsigned UINTb $(α_{q}, β_{q}) = (0, 2^{b} - 1)$ 인 경우
유형 정밀도가 범위를 벗어난 값을 클리핑 한다.
구체적으로, 양자화 진행에서는 추가 클립 단계가 있다.

$x_{q} = c l i p (r o u n d (\frac{1}{s} x + z), α_{q}, β_{q})$

여기서 $c l i p (x, l, u)$ 함수는 다음과 같이 정의 된다.

$c l i p (x, l, u) = {\begin{cases} l i f x < 1 \\ x i f l \leq x \leq u \\ u i f x > u \end{cases}$

Affine Quantization Mapping

위에서 설명한 Quantization Mapping을 Affine Quantization Mapping이라고도 한다.

Scale Quantization Mapping

정수형이 INTb로 부호화되면 $(α_{q}, β_{q}) = (- 2^{b - 1} | 1, 2^{b - 1} - 1)$ 이고, $z = 0$ 을 강제 한다.
수학적으로는 아래와 같다

$α_{q} = - β_{q}$

$r o u n d (\frac{β α_{q} - α β_{q}}{β - α} = 0)$

위 결과 $α = - β$ 가 생성 된다.
따라서, 부동 소수점 범위인 $[α, - α]$ 와 정수 범위 $[α_{q} - β_{q}]$ 사이에서 매핑된다.
0을 중심으로 정확히 대칭이기 때문에, Symmetric Quantization Mapping 이라고도 한다.
Scale Quantization Mapping은 Affine Quantization Mapping의 특수한 경우일 뿐이고, 정수 범위에 사용되지 않는 비트가 존재한다.

요약 (Summary)

Quantization function

$f_{q} (x, s, z) = c l i p (r o u n d (\frac{1}{s} x + z), α_{q}, β_{q})$

de-Quantization function

$f_{d} (x_{q}, s, z) = s (x_{q} - z)$

Quantized Matrix Multiplication

: 추후 작성

Quantized Deep Learning Layers

딥러닝 모델에서는 행렬 곱셈 외에도 ReLU와 같은 비선형 활성화 계층과 배치 정규화 같은 특수 계층이 존재한다.
실제로 양자화 된 딥러닝 모델에서 이러한 계층을 어떻게 처리할 것인가가 가장 중요한 문제이다.

간단한 솔루션

양자화 된 입력 텐서를 레이어로 역 양자화 하고, 일반적인 부동 소수점 계산을 사용하여 출력 텐서를 양자화 하는 것.
모델에 이러한 계층이 몇개만 존재하거나, 계층을 양자화된 방식으로 처리하기 위한 특별한 구현이 없는 경우에 작동한다.

대부분 딥러닝 모델에서 계층의 수는 무시 할 수 없으며, 위와 같은 간단한 솔루션을 사용하면 추론이 느려질 가능성이 크다.

Quantized ReLU

활성화 함수 ReLU를 아래와 같이 정의한다.
기존 ReLU 정의와 다르지만, 더 일반화 되어 양자화 된 ReLU 구현에 편리하다.

$R e L U (x, z_{x}, z_{y}, k) = {\begin{cases} z_{y} i f x \leq z_{x} \\ z_{y} + k (x - z_{x}) i f x \geq z_{x} \end{cases}$

딥러닝 모델에서 일반적으로 사용되는 ReLU는 $z_{x} = 0, z_{y} = 0, k = 1$ 일 때 위 정의의 특수한 경우입니다.

$R e L U (x, 0, 0, 1) = {\begin{cases} 0 i f x \leq 0 \\ x i f x \geq 0 \end{cases}$

ReLU가 수학적으로 어떻게 양자화되었는지 증명해 보겠습니다.

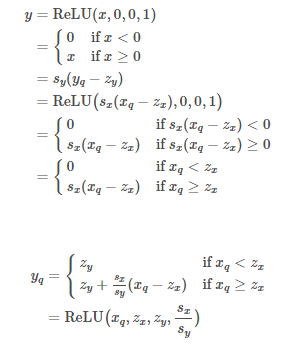
따라서 부동 소수점 $y = R e L U (x, 0, 0, 1)$ 에 해당하는 양자화된 ReLU를 수행하려면 $y_{q} = R e L U (x_{q}, z_{x}, z_{y}, \frac{s_{x}}{s_{y}})$ 만 하면 된다.

양자화된 ReLU 레이어에 대한 소스 코드

import numpy as np


def quantization(x, s, z, alpha_q, beta_q):

    x_q = np.round(1 / s * x + z, decimals=0)
    x_q = np.clip(x_q, a_min=alpha_q, a_max=beta_q)

    return x_q


def quantization_int8(x, s, z):

    x_q = quantization(x, s, z, alpha_q=-128, beta_q=127)
    x_q = x_q.astype(np.int8)

    return x_q


def quantization_uint8(x, s, z):

    x_q = quantization(x, s, z, alpha_q=0, beta_q=255)
    x_q = x_q.astype(np.uint8)

    return x_q


def dequantization(x_q, s, z):

    # x_q - z might go outside the quantization range
    x_q = x_q.astype(np.int32)
    x = s * (x_q - z)
    x = x.astype(np.float32)

    return x


def generate_quantization_constants(alpha, beta, alpha_q, beta_q):

    # Affine quantization mapping
    s = (beta - alpha) / (beta_q - alpha_q)
    z = int((beta * alpha_q - alpha * beta_q) / (beta - alpha))

    return s, z


def generate_quantization_int8_constants(alpha, beta):

    b = 8
    alpha_q = -2**(b - 1)
    beta_q = 2**(b - 1) - 1

    s, z = generate_quantization_constants(alpha=alpha,
                                           beta=beta,
                                           alpha_q=alpha_q,
                                           beta_q=beta_q)

    return s, z


def generate_quantization_uint8_constants(alpha, beta):

    b = 8
    alpha_q = 0
    beta_q = 2**(b) - 1

    s, z = generate_quantization_constants(alpha=alpha,
                                           beta=beta,
                                           alpha_q=alpha_q,
                                           beta_q=beta_q)

    return s, z


def relu(x, z_x, z_y, k):

    x = np.clip(x, a_min=z_x, a_max=None)
    y = z_y + k * (x - z_x)

    return y


def quantization_relu_uint8(x_q, s_x, z_x, s_y, z_y):

    y = relu(x=x_q.astype(np.int32), z_x=z_x, z_y=z_y, k=s_x / s_y)
    y = np.round(y, decimals=0)
    y = np.clip(y, a_min=0, a_max=255)
    y = y.astype(np.uint8)

    return y


if __name__ == "__main__":

    # Set random seed for reproducibility
    random_seed = 0
    np.random.seed(random_seed)

    # Random matrices
    m = 2
    n = 4

    alpha_X = -60.0
    beta_X = 60.0
    s_X, z_X = generate_quantization_int8_constants(alpha=alpha_X, beta=beta_X)
    X = np.random.uniform(low=alpha_X, high=beta_X,
                          size=(m, n)).astype(np.float32)
    X_q = quantization_int8(x=X, s=s_X, z=z_X)
    X_q_dq = dequantization(x_q=X_q, s=s_X, z=z_X)

    alpha_Y = 0.0
    beta_Y = 200.0
    s_Y, z_Y = generate_quantization_uint8_constants(alpha=alpha_Y,
                                                     beta=beta_Y)
    Y_expected = relu(x=X, z_x=0, z_y=0, k=1)
    Y_q_expected = quantization_uint8(x=Y_expected, s=s_Y, z=z_Y)

    Y_expected_prime = relu(x=X_q_dq, z_x=0, z_y=0, k=1)
    Y_expected_prime_q = quantization_uint8(x=Y_expected_prime, s=s_Y, z=z_Y)
    Y_expected_prime_q_dq = dequantization(x_q=Y_expected_prime_q,
                                           s=s_Y,
                                           z=z_Y)

    print("X:")
    print(X)
    print("X_q:")
    print(X_q)

    print("Expected FP32 Y:")
    print(Y_expected)
    print("Expected FP32 Y Quantized:")
    print(Y_q_expected)

    Y_q_simulated = quantization_relu_uint8(x_q=X_q,
                                            s_x=s_X,
                                            z_x=z_X,
                                            s_y=s_Y,
                                            z_y=z_Y)
    Y_simulated = dequantization(x_q=Y_q_simulated, s=s_Y, z=z_Y)

    print("Expected Quantized Y_q from Quantized ReLU:")
    print(Y_q_simulated)
    print("Expected Quantized Y_q from Quantized ReLU Dequantized:")
    print(Y_simulated)

    # Ensure the algorithm implementation is correct
    assert (np.array_equal(Y_simulated, Y_expected_prime_q_dq))
    assert (np.array_equal(Y_q_simulated, Y_expected_prime_q))

결과 값

$ python relu.py 
X:
[[ 5.8576202 25.822723  12.331605   5.385982 ]
 [-9.161424  17.507294  -7.489535  47.01276  ]]
X_q:
[[ 12  55  26  11]
 [-19  37 -16 100]]
Expected FP32 Y:
[[ 5.8576202 25.822723  12.331605   5.385982 ]
 [ 0.        17.507294   0.        47.01276  ]]
Expected FP32 Y Quantized:
[[ 7 33 16  7]
 [ 0 22  0 60]]
Expected Quantized Y_q from Quantized ReLU:
[[ 7 33 16  7]
 [ 0 22  0 60]]
Expected Quantized Y_q from Quantized ReLU Dequantized:
[[ 5.490196 25.882353 12.54902   5.490196]
 [ 0.       17.254902  0.       47.058823]]

Quantization Steps

Layer fusions
: 레이어들을 하나로 묶어주는 단계
: Conv-BatchNorm-ReLU 가 가장 많이 사용되고 있는 layer fusions 이다.
Formula Definition : 양자화를 할 때 사용하는 수식을 정의
: Floating point type ☞ Integer point type (Float32 to Int8) , Quantization
: Integer point type ☞ Floating point type (Int8 to Float32) , Dequantization
HW Deployment
: Depending on the hardware (Calibration)
Dataset Calibration
: 가중치를 변경하기 위한 파라미터를 데이터셋을 이용하여 계산한다.
Weight Conversion
: 가중치를 Floating point type에서 Integer point type으로 변환한다.
Dequantization
: 추론을 통하여 얻은 결과값을 역 양자화를 통해서 다시 Floating point type으로 변경함.

Layer fusions

JINSOL KIM blog 참조 https://gaussian37.github.io/

빨간색은 첫번째 Layer , 파란색은 두번째 Layer를 뜻한다.
첫 줄은 각각 떨어져 있는 Layer들은 Conv2D, BatchNorm, ReLU 3항목 각각 Quantization 적용을 의미한다.
둘째 줄은 Conv2D-BatchNorm-ReLU 한꺼번에 Quantization 적용을 의미한다.

모든 Layer에 Quantization을 적용하지 않는 이유

양자화 횟수를 감소 시키면, 추론 시간과 정밀도와 재현율을 개선할 수 있다.

횟수를 대폭 줄이면 양자화 목적이 사라질 수 있기에 어떤 부분을 Layer Fusions을 할 지를 연구해야 한다.

신경망 정수형 양자화 종류

신경망 양자화에는 3가지 종류가 있다.

Integer Quantization
Dynamic Quantization
Static Quantization

Static Quantization 과 Quantization aware training은 위 항목 중 가장 빠르기 때문에 가장 흔하게 볼 수 있다.

Quantization Modes	Data Requirements	Inference Latency	Inference Accuracy Loss
Dynamic Quantization	None	Usually Faster	Smallest
Static Quantization	Unlabled	Fastest	Smaller
Quantization Aware Training	Labeled	Fastest	Smallest

출처 : Lei Mao blog

Dynamic Quantization

Dynamic Quantization을 사용하는 신경망 추론에서는 최대한 많은 integer ops를 사용한다.
가중치는 런타임 이전에 정수로 양자화 되었다.
Output or Activation Tensor : 부동소수점 텐서
:: Scales 과 Zero points 를 모르기 때문
부동소수점 텐서를 구하면 /( (\alpha, \beta)\)를 찾을 수 있다.
tensor의 경우 Scale과 zero point를 계산하고 런타임 동안 부동소수점 텐서를 동적 정수 텐서로 양자화 한다.

예를 들면, Matrix Multiplication in Dynamic Quantization 의 경우 $X_{q}$ 를 이용하여 $Y_{q, i, j}$ 대신 부동 소수점인 $Y_{i, j}$ 를 계산한다.

$Y_{i, j} = s_{b} (b_{q, j} - z_{b}) + s_{X} s_{W} [(\sum_{k = 1}^{p} X_{q, i, k} W_{q, k, j}) - (z_{W} \sum_{k = 1}^{p} X_{q, i, k}) - (z_{X} \sum {k = 1}^{p} W_{q, k, j}) + p z_{X} z_{W}]$

대부분의 경우 부동 소수점 활성화 텐서를 계산하기 위해 빠른 정수 ops에서 성능을 얻을 수 있다.
위의 표에서 요약한 것처럼 Dynamic Quantization의 장점은 추론에 앞서 어떤 종류의 보정을 수행하기 위해
어떠한 데이터도 필요하지 않다는 것이다.

Static Quantization

Clipping range가 사전에 미리 계산이 되어서 inference 시에는 고정된 값으로 사용되는 방법을 의미한다.
고정된 Clipping range를 사용하기 때문에 이 방법은 추가적인 계산 비용이 발생하지 않지만 Dynamic Quantization
방법에 비해 낮은 성능을 보이곤 한다.
Static Quantization의 Clipping range를 사전에 정하는 대표적인 방법은 샘플 입력 데이터를 준비하여 range를
정해보는 것이다. 이 방법을 Calibration이라고 부른다.

참조자료 링크

https://kaixih.github.io/fused-batch-norm-activation #(Conv-BachNorm-ReLU)
https://www.youtube.com/playlist?list=PLC89UNusI0eSBZhwHlGauwNqVQWTquWqp
https://gaussian37.github.io
https://leimao.github.io/article/Neural-Networks-Quantization/#Introduction
대학원 강의 자료

'AI > Notions' 카테고리의 다른 글

Activation Function : Step/Linear Function (0)	2022.12.27
Perceptron (0)	2022.12.27
CNN (Convolutional Neural Network) 개념 정리 (0)	2022.12.14

내 블로그 - 관리자 홈 전환	`Q` `Q`
새 글 쓰기	`W` `W`

글 수정 (권한 있는 경우)	`E` `E`
댓글 영역으로 이동	`C` `C`

이 페이지의 URL 복사	`S` `S`
맨 위로 이동	`T` `T`
티스토리 홈 이동	`H` `H`
단축키 안내	`Shift` + `/` `⇧` + `/`

기록 일지